جواب صفحه ۵۵ و ۵۶ هندسه دوازدهم ⚜️ سوال متن و مثال با تدریس ویدیویی

پاسخ سوال متن و مثال صفحه ۵۵ و ۵۶ هندسه دوازدهم متوسطه دوم رشته ریاضی فیزیک از فصل ۲ «آشنایی با مقاطع مخروطی» درس «بیضی و سهمی» را با با راه حل‌های صحیح و تصویری در ادامه در بخش آموزش و پرورش ماگرتا برای کمک به شما دانش آموز کوشا آماده کرده‌ایم.

پاسخ صفحه بعدی: جواب صفحه ۵۷ و ۵۸ و ۵۹ هندسه دوازدهم

فیلم آموزشی صفحه ۵۵ و ۵۶ هندسه دوازدهم

در ویدیو زیر می توانید پاسخ صفحه ۵۵ و ۵۶ هندسه دوازدهم را با توضیح کامل مشاهده کنید و مشکلات خود را برطرف کنید. همچنین در ادامه مقاله نیز به این سوالات پاسخ داده شده است.

جواب سوال متن صفحه ۵۵ هندسه دوازدهم

رسم دقیق یک منحنی توسط نرم افزارهای ریاضی انجام می گیرد. طبیعی است که در رسم منحنی ها با کاغذ و قلم، شکل حاصل شکل تقریبی منحنی مورد نظر خواهد بود.
برای رسم یک سهمی ابتدا معادله آن را به صورت استاندارد می نویسیم و با توجه به آن، مختصات رأس سهمی، مقدار a (فاصله کانونی)، مختصات F (کانون) و خط هادی آن را به دست می آوریم و نیز درمی یابیم که دهانه سهمی رو به کدام طرف است.
یکی از مهمترین نقاطی که باید در رسم سهمی جایگاه آن را مشخص نماییم، رأس سهمی است. اگر کانون سهمی را نیز مشخص نماییم دراین صورت خطی که از رأس و کانون سهمی عبور می کند محور تقارن سهمی است.

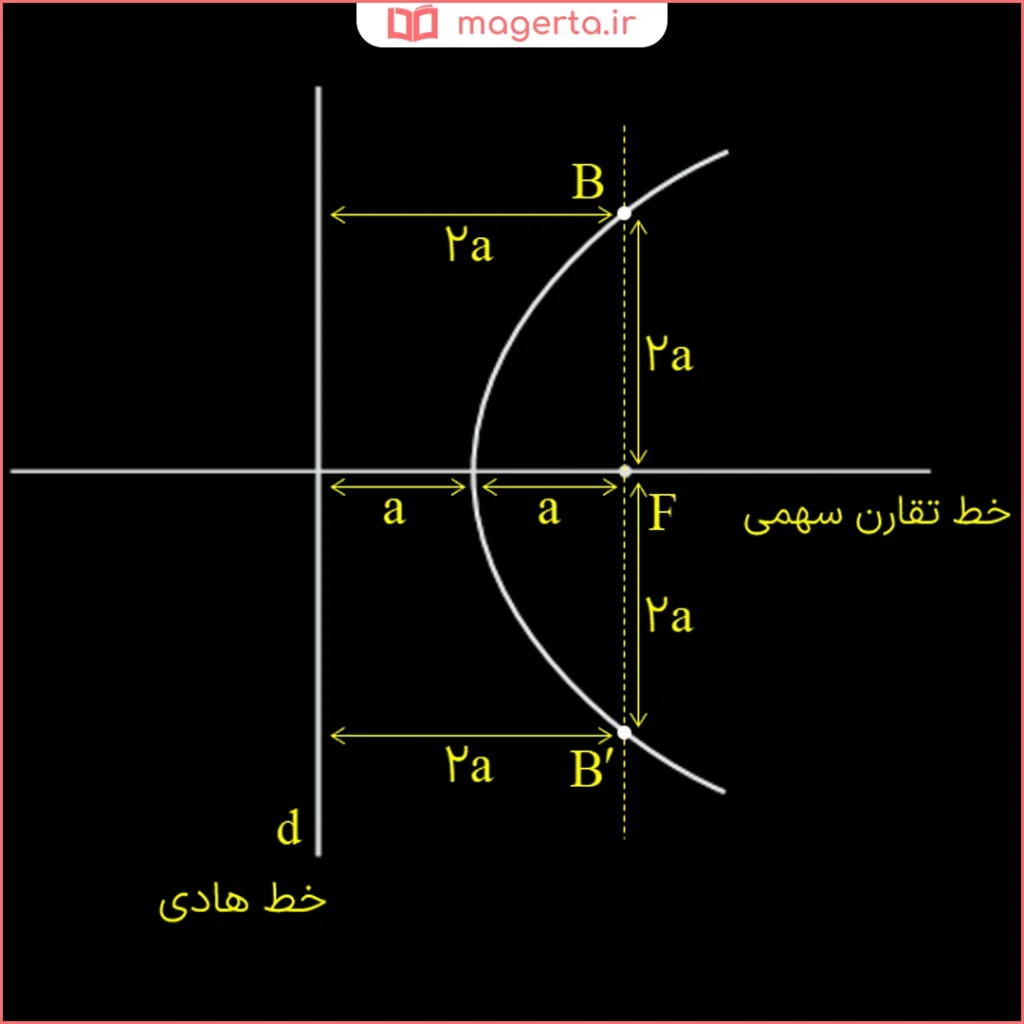
حال اگر خطی را که در نقطه F بر محور تقارن سهمی عمود است رسم کنیم و روی آن دو نقطه، مثلاً B و B’ را که به فاصله 2a از F هستند مشخص نماییم، در این صورت نقاط B و B’ بر سهمی واقع اند. چرا؟

✅ جواب: پاره‌خط (BB’) در نقطۀ (F) بر خط تقارن سهمی عمود است. از آنجا که خط هادی نیز بر همین خط تقارن عمود می‌باشد، خط واصل (FA) خودِ خط تقارن سهمی است که بر خط هادی عمود است. بنابراین پاره‌خط (BB’) با خط هادی موازی خواهد بود و فاصله آن از خط هادی برابر با (2a) است. در نتیجه، نقاط (B) و (B’) نیز از خط هادی به اندازه (2a) فاصله دارند.
بر اساس تعریف مکان هندسی سهمی، هر نقطه‌ای از صفحه (مانند (B) و (B’)) که فاصله‌اش از یک خط ثابت در آن صفحه (خط هادی) و از یک نقطه ثابت خارج از آن خط (کانون (F)) برابر باشد، روی منحنی سهمی قرار می‌گیرد.

جواب مثال صفحه ۵۶ هندسه دوازدهم

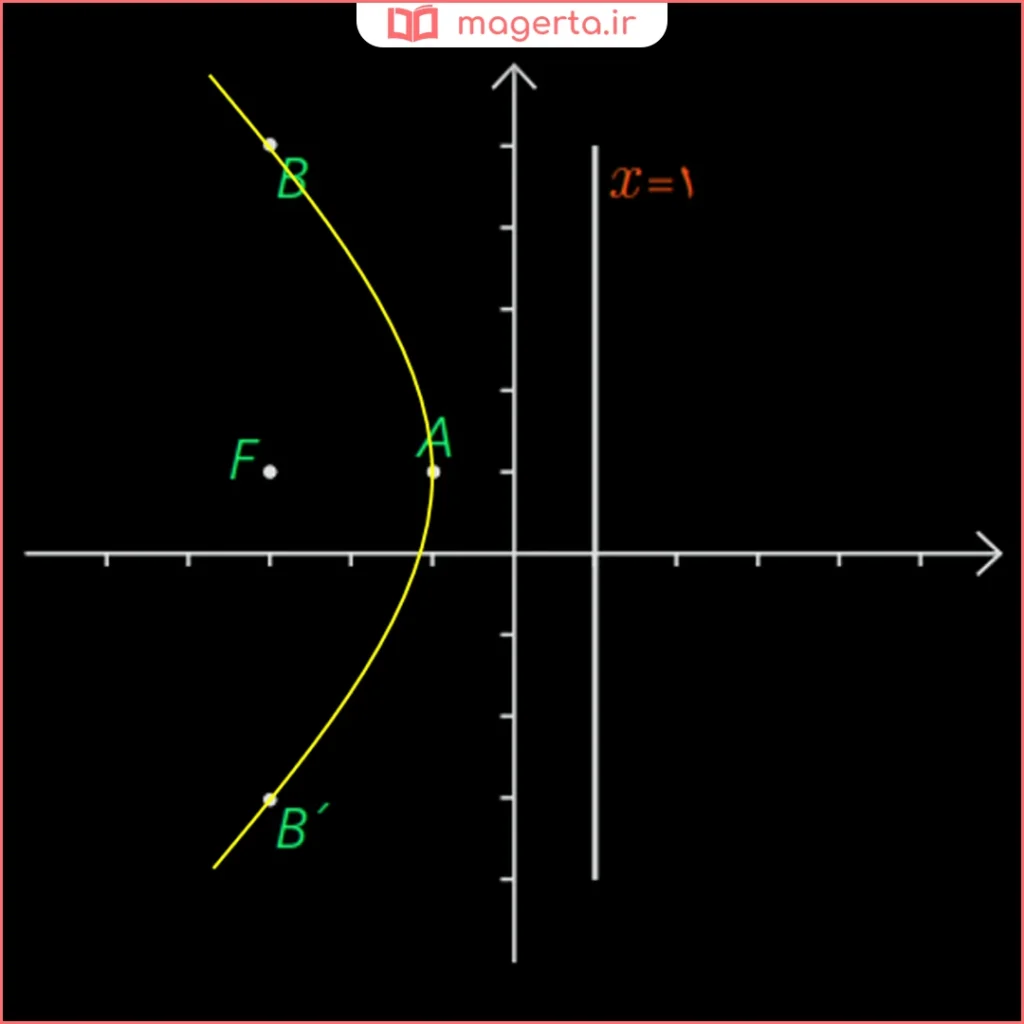
نمودار معادله y^۲−۲y+۸x+۹=۰ را رسم کنید.
در این صورت نقاط B و B’ که هم طول با F و به فاصله ۲a=۴ از F باشند یعنی B(-۳,۵)  و B'(-۳,-۳) نیز بر سهمی واقع اند. فاصله هر یک از آنها را از کانون و خط هادی بررسی کنید. حال با وصل کردن نقاط B و A و B’ به صورت یک منحنی و ادامه آن، شکل تقریبی سهمی موردنظر را به دست آورید.

⚠️ دانش آموز عزیز به این نکته نیز توجه داشته باشید که مطالب درسی قرار گرفته شده در این صفحه فقط جنبه کمک آموزشی دارد لذا قبل از استفاده کردن از آن ها حتما خودتان نیز به سوالات پاسخ دهید تا مفهوم درس را به خوبی متوجه شوید.

پاسخ صفحه قبلی: جواب صفحه ۵۴ هندسه دوازدهم

🔔 در این بخش جواب صفحه ۵۵ و ۵۶ هندسه دوازدهم که مربوط به فصل ۲ می باشد را مرور کردیم، اگر سوالی دارید از بخش نظرات بپرسید. جهت مشاهده پاسخ سایر تمرین های کتاب شماره صفحه آن را به همراه عبارت «ماگرتا» در گوگل جست و جو کنید.