«ثلث» یک واژه عربی به معنی «یکسوم» است و در ریاضی هم دقیقاً همین مفهوم را منتقل میکند: یک قسمت از سه قسمتِ کاملاً مساوی. این مفهوم از پایهترین مباحث کسرهاست و از سالهای ابتدایی مدرسه تا مسائل تناسب، درصد و اندازهگیری به کار میآید.
با وجود سادگیِ تعریف، اشتباهاتی مثل قاطی کردن ثلث با «سهبرابر»، یا برداشت غلط از اعشار تکرارشونده باعث میشود بعضیها در محاسبات روزمره هم خطا کنند. در این مقاله از بخش علمی ماگرتا، ثلث را مرحلهبهمرحله توضیح میدهیم تا هم معنی دقیق آن روشن شود و هم روش محاسبه و کنترل جواب را بلد باشید.

تعریف دقیق ثلث و جایگاه آن در کسرها
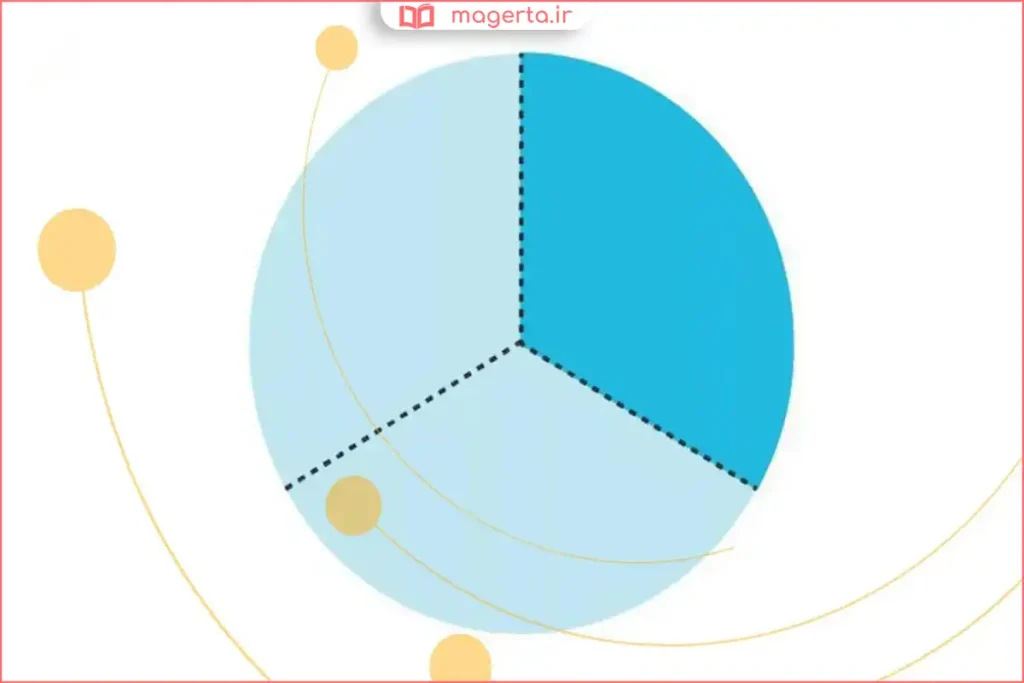
ثلث یعنی «یک از سه»؛ یعنی کل را به سه بخش برابر تقسیم میکنیم و یکی از آن بخشها را برمیداریم. این تعریف هم برای عددها درست است و هم برای شکلها، طولها، زمان و هر کمیتی که قابل تقسیم به سه قسمت مساوی باشد.
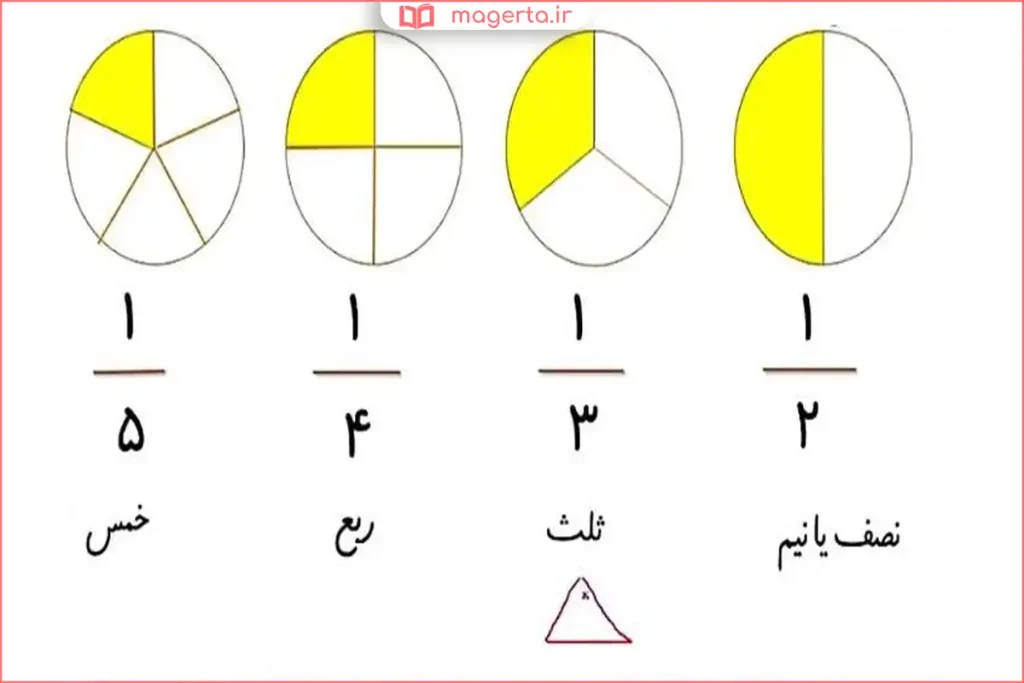
ثلث یک «کسر واحد» است، چون صورت آن ۱ و مخرج آن ۳ است. کسرهای واحد مثل ۱/۲ و ۱/۳ و ۱/۴ پایه یادگیری مقایسه کسرها هستند: هرچه مخرج بزرگتر شود، هر قسمت کوچکتر میشود؛ بنابراین ثلث از ربع بزرگتر و از نصف کوچکتر است.
یک یادآوری کلیدی این است: ثلث یعنی «تقسیم بر ۳» نه «ضرب در ۳». اگر قرار است یکسومِ چیزی را پیدا کنید، دارید مقدار را کوچکتر میکنید، نه بزرگتر.
نمایشهای رایج ثلث
رایجترین نمایش ثلث، کسر ۱/۳ است. این نمایش میگوید از سه قسمت مساوی، یک قسمت مدنظر است.
نمایش دوم، اعشار دورهای است. وقتی ۱ را بر ۳ تقسیم میکنید، نتیجه ۰٫۳۳۳… میشود؛ یعنی عدد ۳ تا بینهایت تکرار میشود. این «…» یعنی ادامه بیپایان الگو و در ریاضی، چنین اعشاری دقیقاً همان مقدار کسر ۱/۳ را نشان میدهد.
نمایش سوم، درصد است. چون ۱/۳ در دستگاه دهدهی پایان ندارد، آن را معمولاً به صورت تقریبی ۳۳٫۳٪ یا ۳۳٫۳۳٪ مینویسند. این نمایش برای تخمینهای سریع مفید است، اما در مسائل دقیق بهتر است همان ۱/۳ باقی بماند.
روش محاسبه ثلث یک عدد
برای محاسبه ثلث یک عدد، آن عدد را بر ۳ تقسیم میکنید. مثال: ثلث ۹ برابر با ۹ ÷ ۳ است و میشود ۳. ثلث ۲۷ هم میشود ۹.
اگر عدد به ۳ بخشپذیر نباشد، جواب میتواند کسری یا اعشاری باشد. مثال: ثلث ۱۰ برابر ۱۰/۳ است و اگر اعشاری بنویسید، میشود ۳٫۳۳۳… در تمرینهای مدرسه معمولاً نوشتن جواب به صورت کسر دقیقتر است و جلوی خطای گرد کردن را میگیرد.
در مسئلههایی که چند مرحله دارند، بهتر است تا آخرِ حل، کسر را نگه دارید. مثلاً اگر ثلث ۱۰ را با ۲ جمع کنید، نوشتن ۱۰/۳ + ۲ دقیقتر از تبدیل زودهنگام به ۳٫۳ است.
مثال تصویری و ملموس
تصور کنید یک کیک گرد یا یک پیتزا دارید:
- اگر آن را به ۳ تکه مساوی تقسیم کنید، هر کدام از این تکهها یک ثلث کیک یا پیتز شماست.
- اگر دو تکه از آن را بردارید، شما دو ثلث (۲/۳) را در دست دارید.
- مجموع هر سه تکه، سه ثلث (۳/۳) میشود که برابر با کل کیک است.
ثلثِ مقدارهای کسری و عددهای مخلوط
اگر مقدار اصلی خودش کسر باشد، باز هم ثلث یعنی تقسیم بر ۳. در کسرها، تقسیم بر ۳ معادل ضرب در ۱/۳ است. مثال: ثلثِ ۳/۴ برابر است با (۳/۴) ÷ ۳ که میشود (۳/۴) × (۱/۳) و نتیجه ۱/۴.
برای عددهای مخلوط، بهتر است ابتدا به کسر تبدیل کنید. مثال: ۱ و ۱/۲ میشود ۳/۲، سپس ثلثِ آن برابر است با ۳/۲ × ۱/۳ که میشود ۱/۲. این روش هم کوتاه است و هم دقیق.
یک نکته عملی این است که در طول محاسبه، سادهسازی را انجام دهید تا عددها بزرگ نشوند. سادهسازی احتمال اشتباه را کم میکند و راه را برای جواب نهایی تمیزتر باز میگذارد.
ثلث در شکلها و اندازهگیری
ثلث یک مفهوم «تقسیم مساوی» است. وقتی میگوییم ثلث یک شکل، یعنی آن شکل را به سه بخش هماندازه تقسیم کنیم و یک بخش را انتخاب کنیم. در رسم و برشهای واقعی، مساوی بودن قسمتها مهمترین معیار است.
در اندازهگیریها، ثلث کاربرد زیادی دارد. مثال: یک ساعت ۶۰ دقیقه است، پس ثلث ساعت یعنی ۲۰ دقیقه. یا اگر طول یک نوار ۹۰ سانتیمتر باشد، ثلث آن ۳۰ سانتیمتر است.
گاهی هم «ثلثِ زاویه» مطرح میشود؛ یعنی یکسوم اندازه زاویه. مثلاً ثلثِ ۹۰ درجه برابر ۳۰ درجه است. از نظر عددی، فقط کافی است اندازه زاویه را بر ۳ تقسیم کنید.
ثلث در مسائل کلامی و تناسبها
در مسائل متنی، ثلث معمولاً به شکل «یکسومِ کل» ظاهر میشود. اگر گفته شود ثلثِ پول خرج شد، یعنی دو ثلث باقی مانده است. اینجا باید دقت کنید که «باقیمانده» خودش یک نسبت جدید است و برابر با ۲/۳ میشود، نه ۱/۳.
در تقسیم مساویِ کار یا هزینه هم ثلث یک مفهوم طبیعی است. اگر سه نفر سهم برابر داشته باشند، سهم هر نفر یکسوم است. مثال: اگر هزینه ۴۵۰ هزار تومان باشد، سهم هر نفر ۱۵۰ هزار تومان میشود.
در بعضی مسئلهها، ثلث با درصد ترکیب میشود. دانستن اینکه ۱/۳ حدود ۳۳٪ است کمک میکند تخمین بزنید، اما اگر مسئله دقت میخواهد، بهتر است محاسبه را با کسر انجام دهید.

کنترل سریع جواب و جلوگیری از اشتباه
یک روش کنترل ساده این است که جواب را در ۳ ضرب کنید و ببینید به مقدار اولیه برمیگردد یا نه. اگر ثلث ۲۷ را ۹ حساب کردهاید، ۹ × ۳ باید ۲۷ شود.
روش کنترل دوم، مقایسه با نصف است. چون ثلث از نصف کوچکتر است، اگر جواب ثلثِ یک عدد بزرگتر از نصف شد، حتماً مسیر را اشتباه رفتهاید. روش سوم هم نگاه به «جهت تغییر» است: ثلثِ یک عدد بزرگتر از ۱ باید از خودِ عدد کوچکتر باشد، نه بزرگتر.
اعشار تکرارشونده و معنی ۰٫۳۳۳…
گاهی گفته میشود ثلث برابر ۰٫۳۳ است، اما این فقط تقریب است. نمایش دقیقِ اعشاریِ ثلث ۰٫۳۳۳… است، یعنی ۳ تا بینهایت تکرار میشود. اگر چند رقم محدود بنویسید، دیگر دقیقاً ۱/۳ نیست.
برای درک سریع، میتوانید یک استدلال کوتاه در ذهن داشته باشید: اگر x برابر ۰٫۳۳۳… باشد، آنگاه ۱۰x برابر ۳٫۳۳۳… میشود و با کم کردن x از ۱۰x به ۹x = ۳ میرسید، پس x = ۱/۳. این نشان میدهد اعشار دورهای فقط یک روش نوشتنِ همان کسر است.
تمرین ذهنی برای سریعتر شدن
اگر میخواهید سریعتر شوید، تشخیص بخشپذیری بر ۳ کمک زیادی میکند: اگر مجموع رقمهای یک عدد بر ۳ بخشپذیر باشد، خودِ عدد هم بر ۳ بخشپذیر است و ثلث آن «تمیز» درمیآید. همچنین میتوانید عدد را بشکنید؛ مثلاً برای ثلث ۷۵، آن را ۶۰ و ۱۵ در نظر بگیرید، ثلث ۶۰ میشود ۲۰ و ثلث ۱۵ میشود ۵، پس جواب ۲۵ است.
یک مهارت دیگر هم این است که بعد از یافتن ثلث، دو ثلث را سریع پیدا کنید. کافی است ثلث را در ۲ ضرب کنید. این کار در مسئلههای «باقیمانده» یا «دو سهم از سه سهم» بسیار پرکاربرد است.
ثلث در عملیات و معادلههای ساده
وقتی وارد محاسباتِ فرمولی میشوید، ثلث فقط یک عدد ثابت نیست، بلکه یک «ضریب» هم میتواند باشد. مثلاً اگر گفته شود ثلثِ x، یعنی x ÷ ۳ یا همان (۱/۳)×x. این نوشتار در جبر مهم است، چون کمک میکند عبارتها را ساده کنید و اشتباه علامت و ترتیب عملیات نداشته باشید.
مثال: اگر x = ۱۸ باشد، ثلثِ x برابر ۶ است. اما اگر عبارت ۳x را اشتباهاً به جای ثلث x در نظر بگیرید، نتیجه ۵۴ میشود و فاصله زیادی با پاسخ درست دارد. به همین دلیل در حل تمرینهای جبر، خواندن دقیق عبارت «ثلثِ x» یا «یکسومِ x» اهمیت بالایی دارد.
در معادلههای ساده هم ثلث زیاد دیده میشود. اگر مسئله بگوید ثلثِ یک عدد برابر ۷ است، شما میدانید عددِ اصلی باید سه برابر ۷ باشد، چون برای برگشت از تقسیم بر ۳، ضرب در ۳ انجام میدهیم. بنابراین عدد ۲۱ است. این نکته نشان میدهد «ثلث گرفتن» و «بازگرداندن از ثلث» دو عمل معکوس هستند.
در جمع و تفریق هم بهتر است ثلث را به شکل کسر نگه دارید. مثال: ثلثِ ۱۲ به اضافه ثلثِ ۹ برابر است با ۱۲/۳ + ۹/۳ که میشود ۲۱/۳ و نتیجه ۷. این روش از کار با اعشار تقریبی دقیقتر است و معمولاً سریعتر هم تمام میشود.
اشتباهات رایج و راههای جلوگیری
یکی از اشتباهات رایج این است که افراد فکر میکنند چون «ثلث» با عدد ۳ ارتباط دارد، پس باید ضرب در ۳ انجام دهند. راه جلوگیری از این خطا، توجه به مفهوم «سهم از کل» است: سهم همیشه کوچکتر از کل است، مگر در شرایط خاصی که کل کمتر از ۱ باشد.
اشتباه رایج دوم، قاطی کردن «ثلثِ کل» با «یکسومِ باقیمانده» است. مثلاً اگر بگویند یکسومِ پول خرج شد و سپس یکسومِ باقیمانده خرج شد، مرحله دوم روی ۲/۳ کل انجام میشود، نه روی کل. اگر این تفاوت را نبینید، جواب نهایی بههم میریزد.
اشتباه سوم، گرد کردن زودهنگامِ ۱/۳ به ۰٫۳۳ است. اگر مسئله چند مرحله دارد، این گرد کردن میتواند خطای قابل توجه ایجاد کند. بهتر است تا حد ممکن با کسر کار کنید و فقط در پایان، اگر نیاز بود، اعشار یا درصد را با دقت مشخص بنویسید.
اشتباه چهارم، تقسیم نابرابر در شکلهاست. وقتی درباره ثلثِ یک شکل صحبت میکنیم، مساوی بودن قسمتها شرط اصلی است. اگر یک مستطیل را به سه قسمت با عرضهای متفاوت تقسیم کنید، هیچکدام ثلث واقعی نیستند، حتی اگر سه تکه داشته باشید. راهکار ساده این است که ابتدا کل طول یا مساحت را بسنجید و بعد با خطکش یا شبکهبندی، سه قسمت برابر بسازید.
کاربردهای ثلث
مفهوم ثلث در زندگی روزمره و شاخههای مختلف ریاضی کاربرد فراوانی دارد:
- تقسیم و سهمبندی: تقسیم ارث، سهام بین شرکا یا تقسیم غذا بین افراد.
- آشپزی و پختوپز: در دستورهای پخت، ممکن است از شما خواسته شود یک سوم لیوان آرد بریزید.
- اندازهگیری: در واحدهای اندازهگیری قدیمی، مثلاً یک سوم متر.
- آمار و احتمالات: محاسبه احتمال وقوع یک رویداد که یکی از سه حالت ممکن است.
خلاصه
به طور خلاصه، ثَلث یک کسر است که نشاندهنده یک بخش از سه بخش مساوی یک کل است و در ریاضیات با نماد ۱/۳ نمایش داده میشود. این مفهوم یکی از اولین و مهمترین قدمها در یادگیری کسرها و نسبتهاست.
پرسش های متداول
ثلث در ریاضی دقیقاً یعنی چه؟
ثلث یعنی یکسومِ یک کل، یعنی یک قسمت از سه قسمت کاملاً مساوی.
ثلث یک عدد را چگونه حساب میکنیم؟
عدد را بر ۳ تقسیم میکنیم و نتیجه را به صورت عدد، کسر یا اعشار مینویسیم.
چرا ۰٫۳۳۳… برابر با ۱/۳ است؟
چون تکرار بینهایتِ ۳ یک اعشار دورهایِ دقیق است و با یک استدلال کوتاه نشان میدهیم مقدارش دقیقاً ۱/۳ میشود.
ثلث ساعت چند دقیقه است؟
چون یک ساعت ۶۰ دقیقه است، ثلث ساعت برابر با ۲۰ دقیقه است.
ثلث از نصف بزرگتر است یا کوچکتر؟
ثلث از نصف کوچکتر است، چون کل را به قسمتهای بیشتری تقسیم میکند و هر قسمت کوچکتر میشود.
نتیجه گیری
ثلث در ریاضی همان یکسوم است و در قالبهای مختلف مثل ۱/۳، ۰٫۳۳۳… و حدود ۳۳٫۳٪ نمایش داده میشود. قاعده اصلی همیشه ثابت است: برای به دست آوردن ثلثِ هر مقدار، آن را بر ۳ تقسیم کنید و با روشهای کنترل مثل ضرب در ۳ یا مقایسه با نصف، پاسخ را بررسی کنید.
وقتی ثلث را به عنوان یک مفهوم «تقسیم مساوی» درک کنید، از مسائل مدرسه تا کاربردهای ساده زندگی مثل زمان و هزینه، محاسبهها برایتان سریعتر و کمخطاتر میشود.
به اشتراک گذاری نظرات شما
کدام بخش از مفهوم ثلث برای شما مبهمتر بود، تبدیل به اعشار یا حل مسئلههای کلامی؟
اگر یک مثال ساده دارید که در آن از یکسوم استفاده کردهاید، آن را بنویسید تا دیگران هم ایده بگیرند.



















