جواب صفحه ۸۲ ریاضی دوازدهم تجربی 🔶 حل کاردرکلاس و فعالیت
گام به گام و حل کار در کلاس و فعالیت صفحه 82 ریاضی دوازدهم علوم تجربی از فصل 4 مشتق درس 2 مشتق پذیری و پیوستگی
پاسخ کار در کلاس و فعالیت صفحه ۸۲ ریاضی دوازدهم متوسطه دوم رشته علوم تجربی از فصل ۴ «مشتق» درس «مشتقپذیری و پیوستگی» را با با راه حلهای صحیح و تصویری در ادامه در بخش آموزش و پرورش ماگرتا برای کمک به شما دانش آموز کوشا آماده کردهایم.
پاسخ صفحه بعدی: جواب صفحه ۸۴ ریاضی دوازدهم تجربی

جواب کاردرکلاس صفحه ۸۲ ریاضی دوازدهم تجربی
در شکلهای زیر مشخص کنید که هر تابع در کدام نقطه یا نقاط مشخص شده مشتقپذیر نیست.
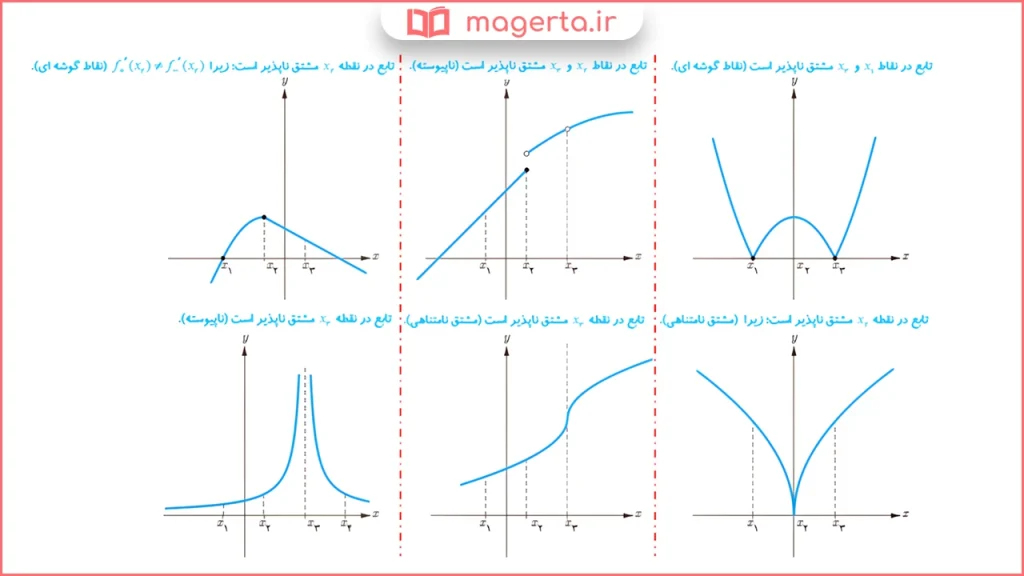
جواب فعالیت صفحه ۸۲ ریاضی دوازدهم تجربی
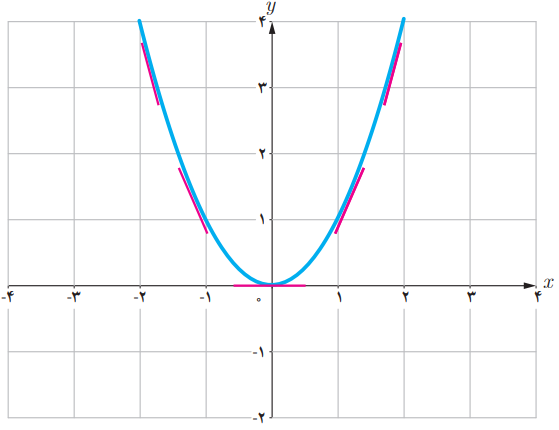
تابع f(x)=x۲ را درنظر می گیریم.
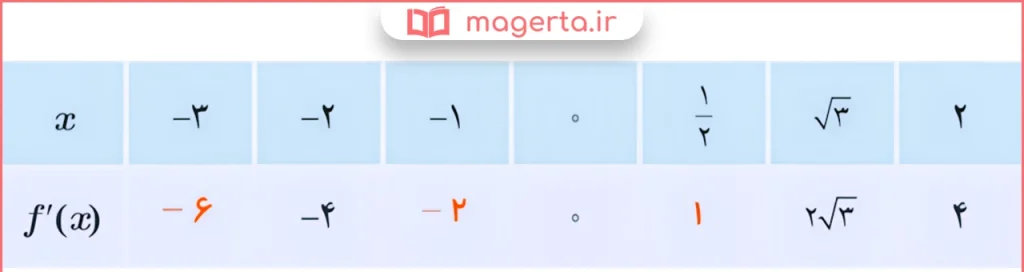
الف) جدول زیر را کامل کنید (مشتق تابع در برخی نقاط حساب شدهاند).
ب) می دانیم مشتق تابع در یک نقطه (در صورت وجود) برابر شیب خط مماس بر منحنی در آن نقطه است و از طرفی مماس بر منحنی در هر نقطه یکتاست، بنابراین f’(x) تابعی از x است.حدس می زنید در چه نقاطی مشتق تابع f(x)=x۲ وجود دارد؟
✅ جواب: با توجه به اینکه نمودار f(x)=x۲ یک منحنی هموار و پیوسته است؛ فرمول مشتق آن، f′(x)=۲x، برای تمام اعداد حقیقی x تعریف شده و مقدار دارد. حدس میزنیم که مشتق تابع f(x)=x۲ در تمام نقاط x که عضو مجموعه اعداد حقیقی (R) هستند، وجود دارد.
⚠️ دانش آموز عزیز به این نکته نیز توجه داشته باشید که مطالب درسی قرار گرفته شده در این صفحه فقط جنبه کمک آموزشی دارد لذا قبل از استفاده کردن از آن ها حتما خودتان نیز به سوالات پاسخ دهید تا مفهوم درس را به خوبی متوجه شوید.
پاسخ صفحه قبلی: جواب صفحه ۷۹ ریاضی دوازدهم تجربی
🔔 در این بخش جواب صفحه ۸۲ ریاضی دوازدهم تجربی که مربوط به فصل ۴ می باشد را مرور کردیم، اگر سوالی دارید از بخش نظرات بپرسید. جهت مشاهده پاسخ سایر تمرین های کتاب شماره صفحه آن را به همراه عبارت «ماگرتا» در گوگل جست و جو کنید.



















