جواب تمرین صفحه ۵۷ و ۵۸ و ۵۹ هندسه دوازدهم

پاسخ تمرین صفحه 57 و 58 و 59 هندسه دوازدهم ریاضی از فصل دوم آشنایی با مقاطع مخروطی درس «بیضی و سهمی» را در ادامه در بخش آموزش و پرورش ماگرتا برای شما دانش آموز عزیز فراهم کرده‌ایم.

همچنین مشاهده کنید: جواب فعالیت صفحه ۵۲ هندسه دوازدهم

پاسخ تمرین صفحه 57 هندسه دوازدهم

1- دو نقطهٔ A و B روی یک بیضی و F و ′F کانون‌های بیضی‌اند. A به کانون F نزدیک‌تر و B به کانون F نزدیک‌تر است. اگر AF′=BF باشد، نشان دهید:

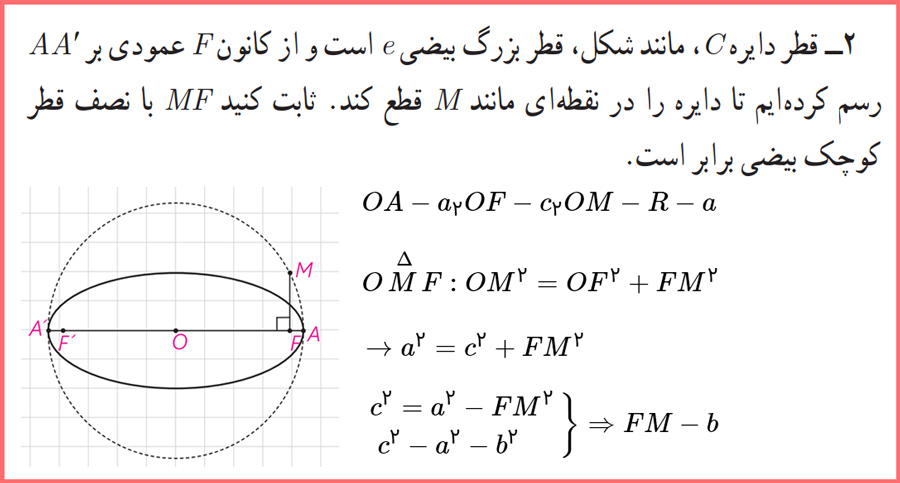
2- قطر دایره C، مانند شکل، قطر بزگ بیضی e است و از کانون F عمودی بر ′AA رسم کرده‌ایم تا دایره را در نقطه‌ای مانند M قطع کند. ثابت کنید MF با نصف قطر کوچک بیضی برابر است.

3- در شکل زیر نقطهٔ M روی بیضی و کانون‌های F و ′F مشخص شده‌اند. خط d را به گونه‌ای رسم کنید که در نقطهٔ M بر بیضی مماس باشد و سپس از نقطهٔ F خطی موازی با MF رسم کنید تا خط d را در نقطه‌ای مانند N قطع کند. ثابت کنید ′NF′=MF

4- نقطهٔ M روی بیضی به اقطار 6 و 10 واحد به گونه‌ای قرار دارد که فاصلهٔ آن تا مرکز بیضی برابر 4 واحد است.
الف) نشان دهید ′OM=OF=OF.
ب) نشان دهید مثلث ′MFF قائم‌الزاویه است.
ج) طول‌های MF و ′MF را به‌دست آورید.

حل تمرین صفحه 58 هندسه دوازدهم

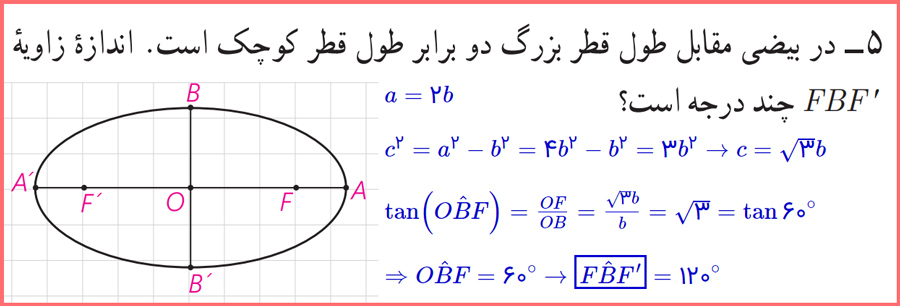
5- در بیضی زیر طول قطر بزرگ دو برابر طول قطر کوچک است. اندازهٔ زاویهٔ ′FBF چند درجه است؟

6- در بیضی زیر ′AA و ′BB دو قطراند. خط d در نقطهٔ B بر بیضی مماس است. پاره‌خط BF را رسم می‌کنیم و در نقطهٔ F عمودی بر BF رسم می‌کنیم تا خط d را در نقطهٔ C قطع کند و از C عمودی بر امتداد قطر بزرگ بیضی رسم می‌کنیم تا آن را در نقطه‌ای مانند D قطع کند. مقدار AD/AF را به‌دست آورید.

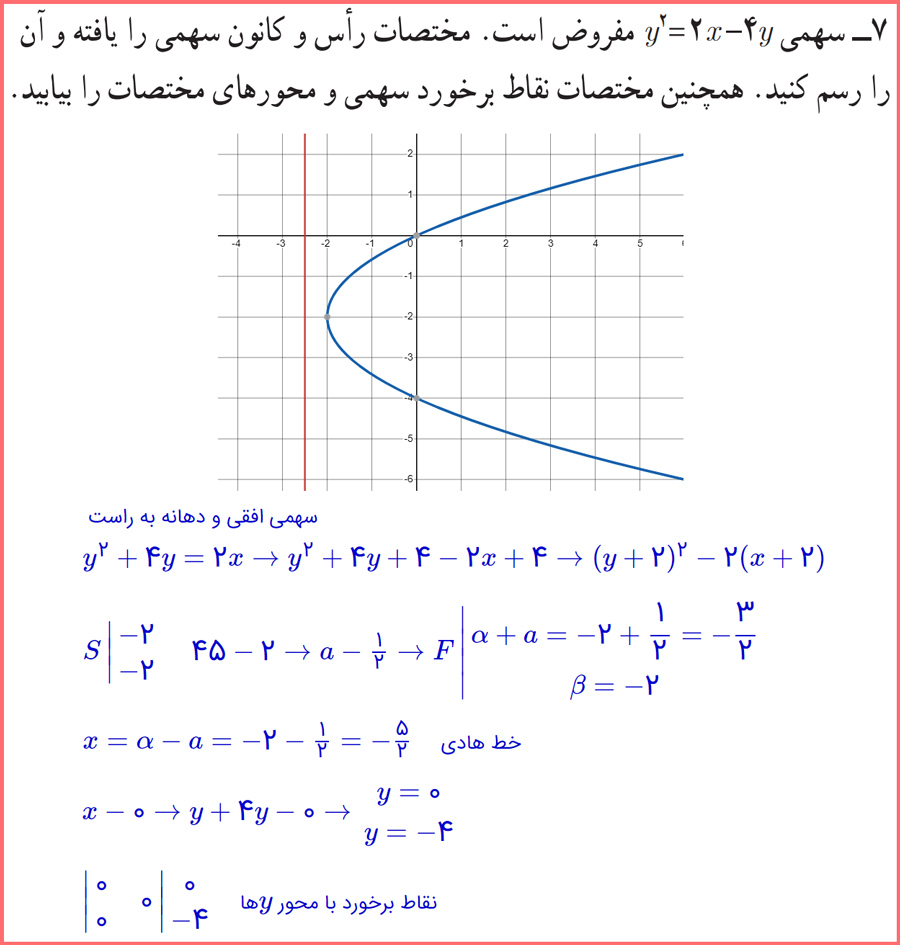
7- سهمی y²=2x−4y مفروض است. مختصات رأس و کانون سهمی را یافته و آن را رسم کنید. همچنین مختصات نقاط برخورد سهمی و محورهای مختصات را بیابید.

8- مختصات رأس و کانون سهمی به معادله (a≠0) y=ax²+bx+c را به‌دست آورید.

9- معادله سهمی را بنویسید که S(1,2) رأس و F(1,−2) کانون آن باشد.

10- سهمی y²=4x−4 مفروض است. به مرکز کانون سهمی و به شعاع 3 واحد دایره‌ای رسم می‌کنیم، مختصات نقاط برخورد دایره و سهمی را بیابید.

11- سهمی P با کانون F و خط هادی d مفروض است. ثابت کنید مرکز هر دایره که از F بگذرد و بر خط d مماس باشد روی سهمی است و برعکس هر نقطه روی سهمی، مرکز یک دایره است که از F گذشته و بر d مماس است. با توجه به این موضوع تعریف دیگری از سهمی ارائه دهید.

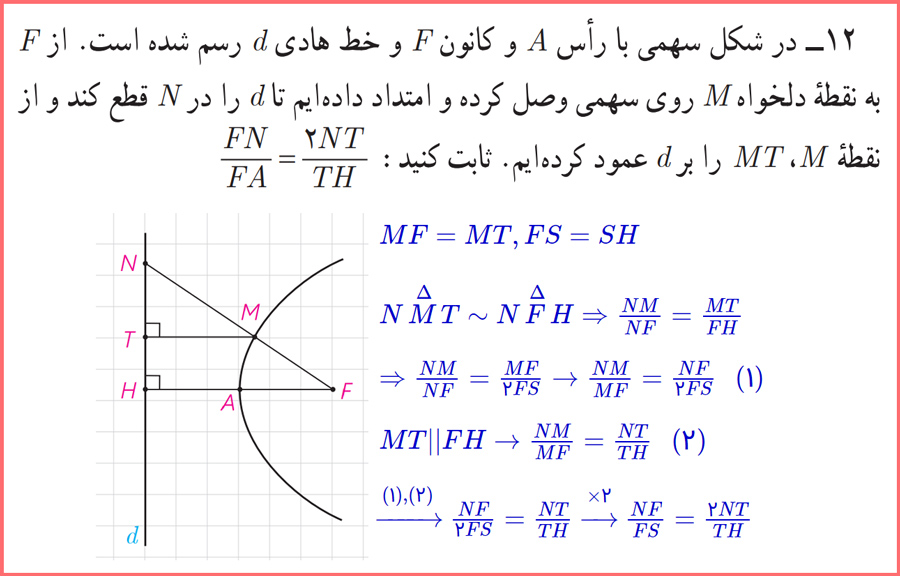
12- در شکل سهمی با رأس A و کانون F و خط هادی d رسم شده است. از F به نقطهٔ دلخواه M روی سهمی وصل کرده و امتداد داده‌ایم تا d را در N قطع کند و از نقطهٔ M و MT را بر d عمود کرده‌ایم. ثابت کنید:

جواب تمرین صفحه 59 هندسه دوازدهم

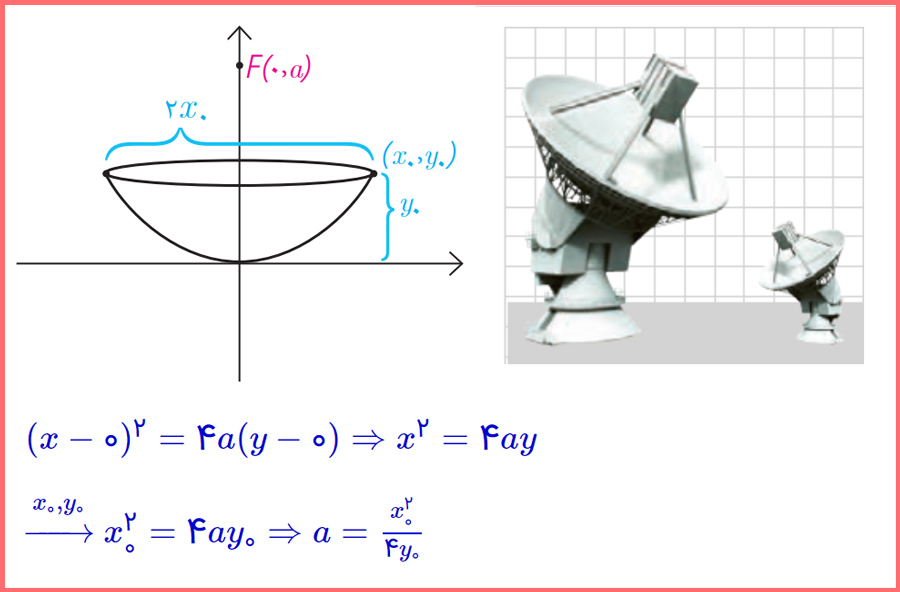
13- یک دانش‌آموز با دیدن دو دیش مخابراتی با ابعاد متفاوت و مشاهدهٔ فاصلهٔ کانونی متفاوت آنها به این فکر افتاد که چگونه می‌توان با داشتن یک دیش فاصلهٔ کانونی آن را به‌دست آورد. او از معلمش خواست که فرمولی برای محاسبهٔ فاصلهٔ کانونی یک دیش به او بگوید. معلم به او گفت: باید قطر دهانهٔ دیش را در خودش ضرب کرد و حاصل ضرب را بر اندازهٔ گودی (عمق) دیش تقسیم کرد و عدد حاصل را بر 16 تقسیم کرد. حاصل فاصلهٔ کانونی دیش است. دلیل درستی این دستور را با توجه به سهمی رسم شده در شکل زیر و فرمول سهمی توضیح دهید.

14- فرض کنید از مثلث ABC، اندازه ضلع BC و ارتفاع AH و محیط مثلث، داده شده باشد، با استفاده از خواص بیضی شیوهٔ رسم این مثلث را توضیح دهید.

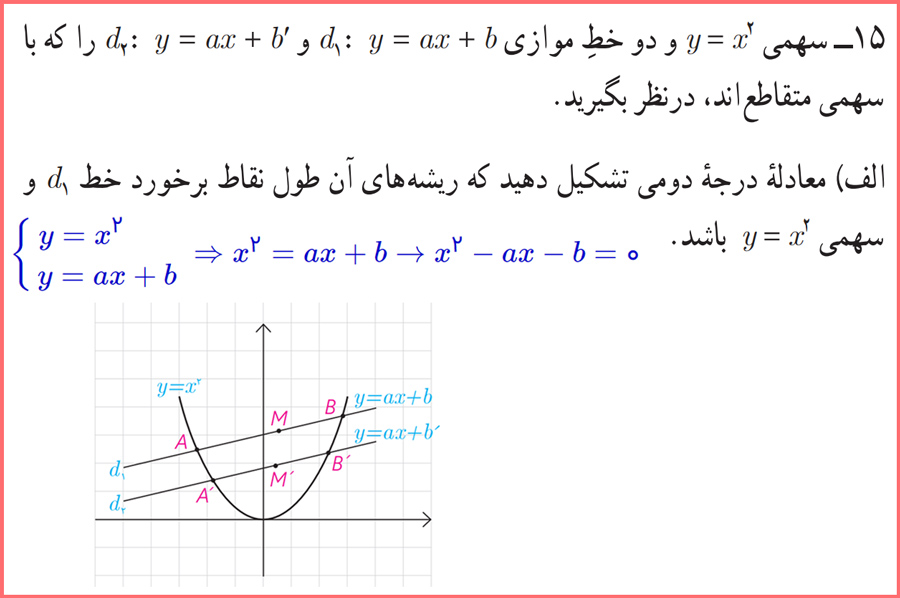
15 – سهمی y=x² و دو خطِ موازی داده شده را که با سهمی متقاطع‌اند، درنظر بگیرید. به سوالات زیر پاسخ دهید.

⭕️ نکته: دانش آموز عزیز مطالب درسی قرار گرفته شده در این سایت فقط جنبه کمک آموزشی دارد و شما نباید از آن ها به شیوه نادرست استفاده نمایید، لذا قبل مشاهده جواب ها یکبار خودتان به سوالات پاسخ دهید سپس اگر مشکلی داشتید از این جواب ها کمک بگیرید.

☑️ به پایان جواب تمرین صفحه ۵۷ و ۵۸ و ۵۹ هندسه دوازدهم رشته ریاضی فیزیک رسیدیم، برای مشاهده حل تمرین سایر صفحات کتاب کافیست آن را در گوگل به همراه عبارت «ماگرتا» جست و جو کنید. همچنین می توانید از بخش نظرات نیز با ما در ارتباط باشید.