جواب صفحه ۶۶ ریاضی ششم✔️ فعالیت + تدریس ویدئویی

پاسخ فعالیت صفحه ۶۶ ریاضی ششم ابتدایی از فصل ۴ «تقارن و مختصات» درس «مرکز تقارن و تقارن مرکزی» را با با راه حل‌های صحیح و توضیحات تصویری و ویدئویی در ادامه در بخش آموزش و پرورش ماگرتا برای کمک به شما دانش آموز کوشا آماده کرده‌ایم.

پاسخ صفحه بعدی: جواب صفحه ۶۷ ریاضی ششم

توضیح صفحه ۶۶ ریاضی ششم

در ویدیو زیر می توانید پاسخ فعالیت صفحه ۶۶ ریاضی ششم را با توضیح کامل مشاهده کنید و مشکلات خود را برطرف کنید. همچنین در ادامه مقاله نیز به این سوالات به صورت تصویری پاسخ داده شده است.

جواب فعالیت صفحه ۶۶ ریاضی ششم

۱- در هریک از شکل های زیر، ابتدا حدس بزنید نقطه‌ی مشخص شده مرکز تقارن شکل است یا نه. سپس درستی حدس خود را بررسی کنید.

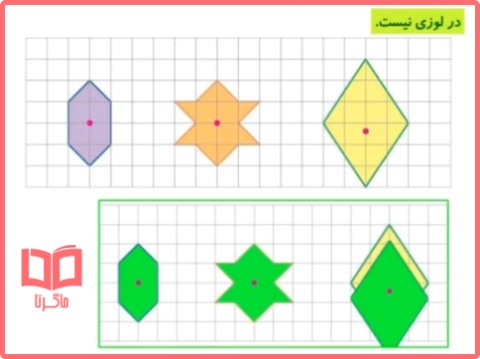
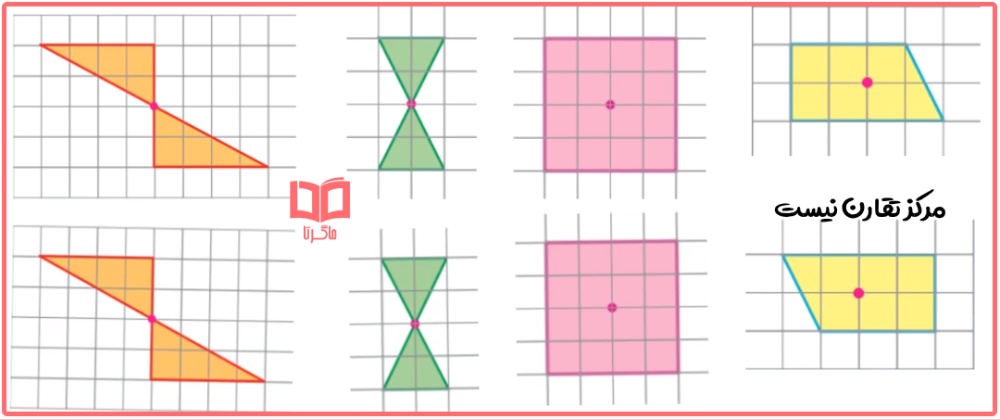
۲- در کدام یک از شکل های زیر، نقطه‌ی مشخص شده، مرکز تقارن نیست؟

۳- خانم جلالی، با استفاده از کاغذ شفاف، قرینه‌ی نقطه‌ی «آ» را نسبت به نقطه‌ی «ب» پیدا کرد و از دانش آموزان خواست قرینه‌ی نقطه‌ی «آ» را با روش دیگری پیدا کنند.

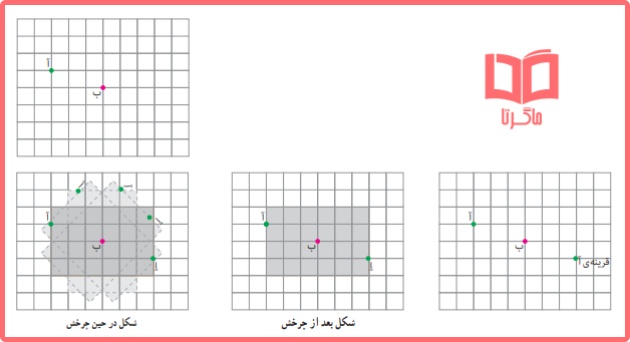
چند دانش آموز روش های زیر را پیشنهاد کرده اند.

علی: قرینه‌‌ی «آ» را نسبت به محور عمودی (قرمز) به دست آورد و آن را «پ» نامید. سپس قرینه‌ی نقطه ی «پ» را نسبت به محور افقی (آبی) پیدا کرد و آن را «ت» نامید. اکنون نقطه‌ی «ت» قرینه‌ی نقطه‌ی «آ» است.

محمد مهدی: نقطه‌ی «آ» را با خط کش به نقطه‌ی «ب» وصل کرد و به همان اندازه ادامه داد و قرینه‌ی آن را پیدا کرد.

سبحان: با شمردن مربع ها از نقطه‌ی «آ» سه واحد به سمت راست و یک واحد به سمت پایین رفت تا به نقطه «ب» رسید. سپس از نقطه‌ی «ب» یک واحد به سمت پایین و سه واحد به سمت راست حرکت کرد تا قرینه‌ی «آ» را پیدا کند.

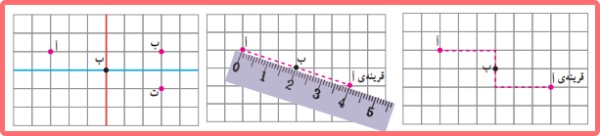
الف) روش های بالا را با هم مقایسه کنید.
✅ جواب: همه روش ها صحیح است و به جواب می رسد اما روشی که سبحان استفاده کرده است بهتر است چون سریع تر به جواب می رسد اما بدی این روش این است که فقط در صفحه شطرنجی می توان از آن استفاده کرد.

ب) توضیح دهید چگونه قرینه‌ی پاره خط «آ ب» نسبت به نقطه‌ی «م» را پیدا کردیم.

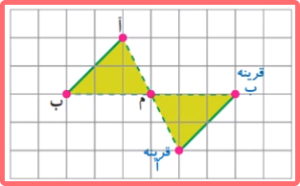
✅ جواب: خط را به شکلی که از نقطه «آ» و «م» رد بشه قرار داده ایم، سپس به میزان فاصله نقطه «آ» تا «م» از نقطه «م» ادامه می دهیم. با این کار قرینه نقطه «آ» را به دست می آوریم. این بار خط کش را طوری قرار می دهیم که از نقطه «ب» و «م» عبور بکند. سپس به میزان فاصله نقطه «ب» از «م» یعنی ۳ واحد از نقطه «م» ادامه می دهیم تا قرینه نقطه «ب» به دست بیاید. در نهایت این دو نقطه را به هم متصل می کنیم تا قرینه پاره خط «آ ب» به دست آید.

پ) قرینه‌ی شکل های زیر را نسبت به نقطه‌ی داده شده پیدا کنید.

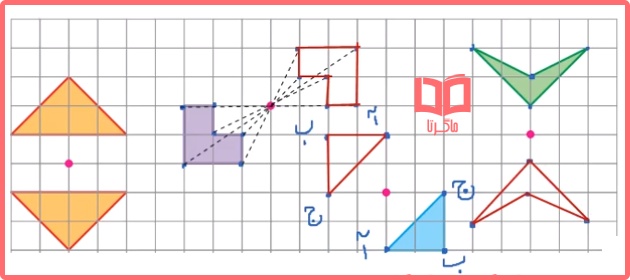
✅ جواب: برای اینکه قرینه یک شکل را نسبت به نقطه ای پیدا کنیم ابتدا باید گوشه‌ها را مشخص کنیم، بعد قرینه گوشه های مشخص شده را نسبت به نقطه موردنظر پیدا کنیم و در آخر آن ها را مثل شکل اولیه به هم وصل کنیم.

⚠️ دانش آموز عزیز به این نکته نیز توجه داشته باشید که مطالب درسی قرار گرفته شده در این صفحه فقط جنبه کمک آموزشی دارد لذا قبل از استفاده کردن از آن ها حتما خودتان نیز به سوالات پاسخ دهید تا مفهوم درس را به خوبی متوجه شوید.

پاسخ صفحه قبلی: جواب صفحه ۶۵ ریاضی ششم

🔔 در این بخش جواب صفحه ۶۶ ریاضی ششم که مربوط به فصل ۴ می باشد را مرور کردیم، اگر سوالی دارید از بخش نظرات بپرسید. جهت مشاهده پاسخ سایر تمرین های کتاب شماره صفحه آن را به همراه عبارت «ماگرتا» در گوگل جست و جو کنید.