جواب فعالیت صفحه ۱۴۶ ریاضی هشتم

جواب صفحه ۱۴۶ ریاضی هشتم : در این قسمت به حل گام به گام جواب فعالیت صفحه 146 ریاضی هشتم متوسطه مربوط به زاویه های محاطی از فصل ۹ دایره را برای تان کامل در بخش آموزش و پرورش ماگرتا برای شما دانش آموز فعال و کوشا آماده کرده ایم.

مطلب پیشنهادی : جواب تمرین صفحه ۱۴۵ ریاضی هشتم

جواب فعالیت صفحه ۱۴۶ ریاضی هشتم

در پاسخ به فعالیت صفحه 146 ریاضی هشتم داریم :

۱- مانند نمونهٔ رسم شدهٔ (الف) در شکل‌های زیر نمونه‌ای از هر یک از وضعیت‌های مختلف یک زاویه و دایره را رسم کنید.

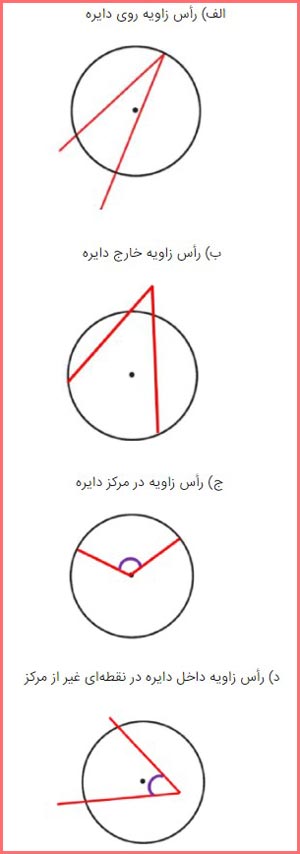
در کدام وضعیت زاویهٔ مرکزی نشان داده شده است؟ ج

به زاویه‌ای که در شکل «الف» مشاهده می‌کنید، زاویهٔ محاطی گفته می‌شود. رأس این زاویه روی دایره است وضلع‌های آن، دایره را قطع کرده‌اند.

۲- اندازهٔ زاویهٔ مرکزی BOC را برحسب BC⌢ بنویسید: 

BOC=⌢BC∧

چرا زاویه‌های A و C در مثلث AOC با هم برابرند؟ چون مثلث متساوی‌الساقین است.

چه ارتباطی میان زاویه BOC و این دو زاویه وجود دارد؟
اندازه هر زاویه خارجی با مجموع دو زاویه داخلی غیر مجاور برابر است.

∧BOC=ˆA+ˆC

اندازهٔ زاویهٔ محاطی BAC را برحسب BC⌢ بنویسید.

BAC = ⌢BC/۲∧

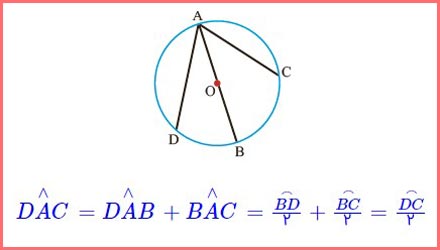
۳- با توجه به فعّالیت قبل با پر کردن جاهای خالی اندازهٔ زاویهٔ محاطی DAC را برحسب DC⌢ بنویسید.

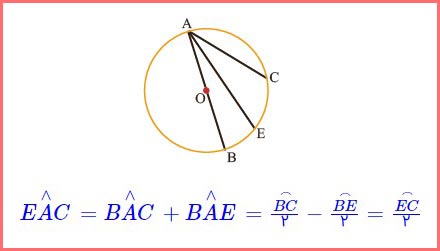
۴- با پر کردن جاهای خالی، اندازهٔ زاویهٔ محاطی EAC را هم برحسب EC⌢ بنویسید.

۵- پاسخ فعّالیت‌های (۲)، (۳)، و (۴) را با هم مقایسه کنید. آیا در این سه فعّالیت، همهٔ حالت‌های زاویهٔ محاطی بررسی شده‌اند؟ بله
عبارت زیر را کامل کنید.

اندازهٔ هر زاویهٔ محاطی برابر است با نصف کمان رو‌به‌ روی آن.

🚀 اگر در هر صفحه ای از کتاب ریاضی هشتم دبیرستان مشکل و یا ایراد درسی داشتید حتما برای ما در قسمت دیدگاه بنویسید تا ما در اسرع وقت بتوانیم به سوال شما پاسخ بدهیم و مشکلات درسی شما دانش آموزان پایه هشتمی های گرامی را حل نماییم.

⚠ نکته : برای حل مسائل ریاضی حتما قلم و کاغذ کنار در خود داشته باشید تا به تمرین کردن بپردازید تا کامل کتاب ریاضی را یاد بگیرید. این یکی از بهترین روش های ثابت شده حل مسئله ریاضی است.

مطلب پیشنهادی : جواب کاردرکلاس صفحه ۱۴۴ ریاضی هشتم

💢 در این بخش جواب فعالیت صفحه ۱۴۶ ریاضی هشتم را مرور کردیم، شما می توانید با اضافه کردن عبارت ماگرتا در آخر جستجوهای درسی تان در گوگل به بهترین پاسخ ها دسترسی پیدا کنید. به یاد داشته باشید که حتما اول خودتان جواب سوال ها را بدهید و برای بررسی درست یا نادرست بودن آن به این پاسخ ها مراجعه کنید. اگر سوالی دارید آن را از قسمت دیدگاه بپرسید تا معلمان و کارشناسان ما به آن پاسخ بدهند. 👍🤗