جواب فعالیت صفحه ۳۹ ریاضی نهم ✍️ با تدریس ویدیویی

جواب صفحه ۳۹ ریاضی نهم از فصل سوم، درس دوم «آشنایی با اثبات در هندسه» و پاسخ فعالیت صفحه 39 ریاضی پایه نهم متوسطه را در ادامه در بخش آموزش و پرورش ماگرتا برای شما دانش آموز کوشا آماده کرده ایم.

پاسخ صفحه بعدی: جواب صفحه ۴۰ ریاضی نهم

توضیح صفحه 39 ریاضی نهم

در ویدیو زیر می توانید پاسخ فعالیت صفحه 39 را با توضیح کامل مشاهده کنید و مشکلات خود را برطرف کنید. همچنین در ادامه مقاله نیز به این سوالات پاسخ داده شده است.

پاسخ فعالیت صفحه ۳۹ ریاضی نهم

۱- در مسئله زیر، فرض و حکم را بنویسید و اشکال استدلال داده شده را بیابید، سپس استدلال درستی برای آن بنویسید.
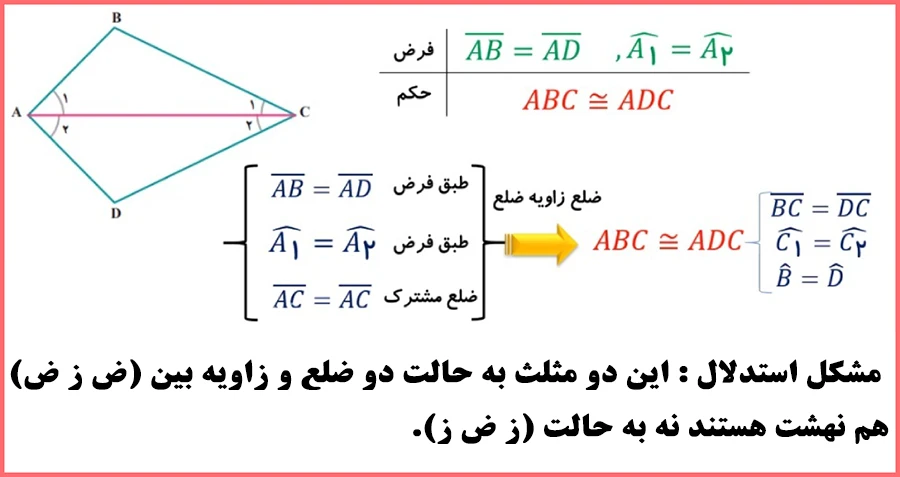
مسئله: در شکل مقابل پار خط AC نیمساز زاویه A است و اضلاع AB و AD برابرند. ثابت کنید مثلث‌های ABC و ADC هم نهشت‌اند.

استدلال: چون AC نیمساز است، داریم A_۱ = A_۲ و C_۱ = C_۲ و از طرفی AC نیز ضلع مشترک در هر دو مثلث است، لذا دو مثلث ABC و ADC به حالت دو زاویه و ضلع بین (ز ض ز) هم نهشت اند.

۲- مثلث زیر متساوی الساقین و AD نیمساز وارد بر قاعده آن است. با استدلال زیر نشان داده ایم که نیمساز وارد بر قاعده، میانه نیز می باشد. لذا نقطه D وسط BC است و AD میانه است. آیا در مثلث ABC می توان نتیجه گرفت که نیمساز زاویه B نیز میانه ضلع مقابل آن است.

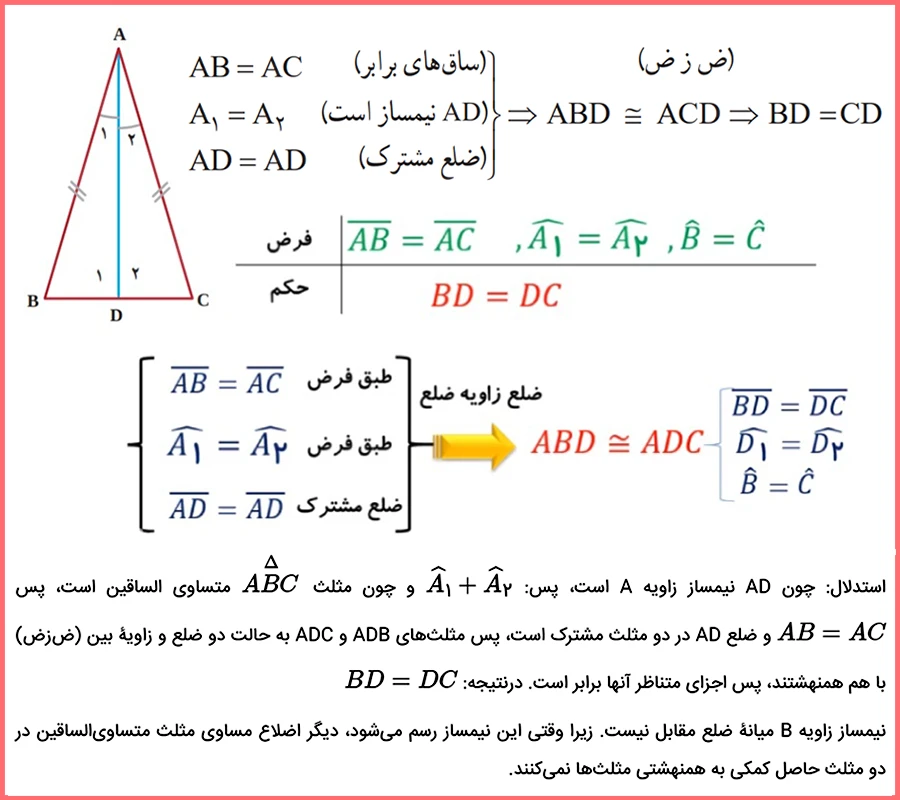
به عبارتی، آیا می توان خاصیت اثبات شده برای نیمساز A را به نیمساز دیگر تعمیم داد؟
✅ نیمساز زاویه B میانه ضلع مقابل نیست. زیرا وقتی این نیمساز رسم می شود، دیگر اضلاع مساوی مثلث متساوی الساقین در دو مثلث حاصل کمکی به همنهشتی مثلث ها نمی کنند.

۳- با استدلال زیر به سادگی می توان نتیجه گیری کرد که قطر AC از مربع ABCD نیمساز زاویه های A و C است. چون دو مثلث ABC و ADC به حالت سه ضلع هم نهشت اند و زوایای متناظر با هم برابر‌ند؛ بنابراین A_۱ = A_۲ و C_۱ = C_۲ و لذا AC نیمساز است.

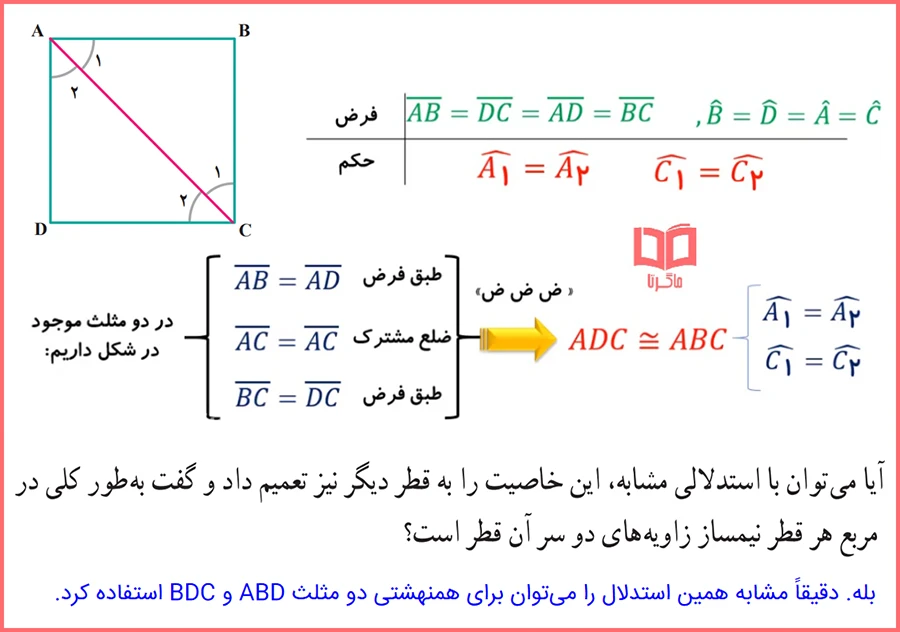
آیا می توان با استدلالی مشابه، این خاصیت را به قطر دیگر نیز تعمیم داد و گفت به طور کلی در مربع هر قطر نیمساز زاویه های دو سر آن قطر است؟
✅ بله. می شود مشابه همین استدلال را برای همنهشتی دو مثلث ABD و BDC به کار برد.

پاسخ سوالات فعالیت صفحه ۴۰ ریاضی نهم

۴- به نظر شما چرا در فعاليت ۲ خاصيت موردنظر قابل تعميم به نيمسازهای ديگر نبود؛ اما در فعاليت ۳ خاصيت موردنظر به قطر ديگر تعميم داده می شود؟
✅ زیرا در در فعالیت ۱، فرض برابری دو ساق مثلث در مورد نیمسازهای دیگر قابلیت استفاده نداشت ولی در فعالیت ۲ مانند ویژگی هایی که برای یک قطر وجود دارد، برای قطر دیگر هم وجود دارد و استفاده می شود.

۵- نقطه ای مانند P، روی عمود منصف پاره خط AB در نظر می گیریم و به دو سر پاره خط وصل می کنیم. چون دو مثلث AHP و BHP به حالت (ض ز ض) هم نهشت اند، نتیجه می گیریم پاره خط های PA و PB با هم برابر است. بنابراین فاصله نقطه P، که روی عمود منصف پاره خط AB است، از دو سر پاره خط AB یکسان اند.

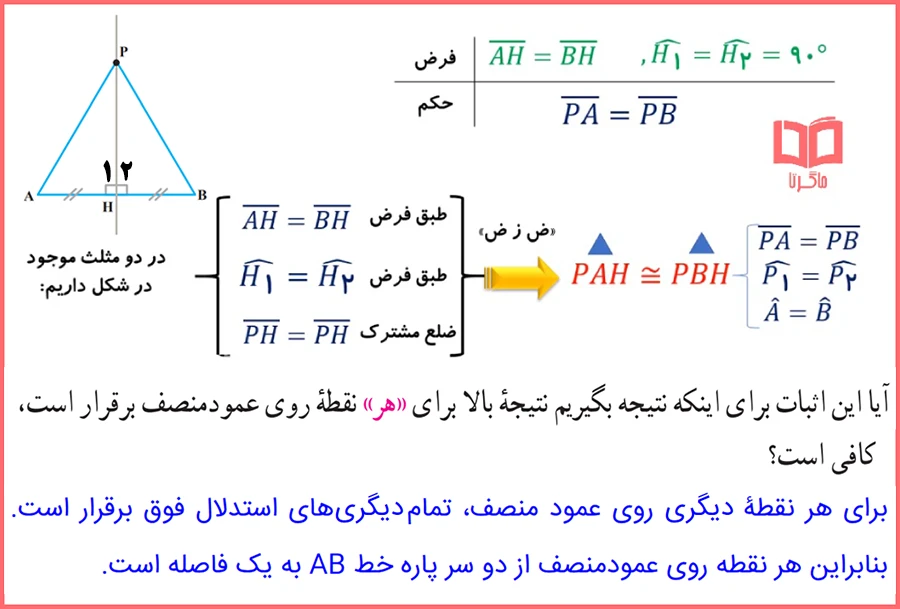
آیا این اثبات برای اینکه نتیجه بگیریم نتیجه بالا برای «هر» نقطه روی عمودمنصف برقرار است، کافی است؟
✅ همه ویژگی های استدلال بالا برای هر نقطه دیگه ای روی عمود منصف قابل استفاده است پس هر نقطه روی عمودمنصف از دو سر پاره خط AB به یک فاصله است.

❤️ دانش آموز عزیز مطالب این صفحه صرفا جنبه کمک آموزشی دارد و شما برای استفاده از آن ها باید یک بار خودتان تمامی سوالات این صفحه را حل کنید سپس اگر مشکلی داشتید از این مطالب کمک بگیرید. با این کار در امتحان و پرسش های کلاسی دچار مشکل نخواهید شد.

پاسخ صفحه قبلی: جواب صفحه ۳۸ ریاضی نهم

🔚 اگر سوالی در رابطه با جواب فعالیت صفحه ۳۹ ریاضی نهم دارید آن را از قسمت دیدگاه بپرسید. همچنین جهت مشاهده گام به گام سایر صفحات کتاب کافیست آن را به همراه عبارت «ماگرتا» در گوگل جست و جو نمایید.