جواب صفحه ۱۲۲ و ۱۲۳ ریاضی دهم ❤️ حل کاردرکلاس با تدریس ویدیویی

پاسخ کار در کلاس صفحه ۱۲۲ و ۱۲۳ ریاضی دهم متوسطه دوم رشته ریاضی فیزیک و علوم تجربی از فصل ۶ «شمارش، بدون شمردن» درس «شمارش» را با با راه حل‌های صحیح و تصویری در ادامه در بخش آموزش و پرورش ماگرتا برای کمک به شما دانش آموز کوشا آماده کرده‌ایم.

پاسخ صفحه بعدی: جواب تمرین صفحه ۱۲۴، ۱۲۵ و ۱۲۶ ریاضی دهم

فیلم آموزشی صفحه ۱۲۲ و ۱۲۳ ریاضی دهم

در ویدیو زیر می توانید پاسخ صفحه ۱۲۲ و ۱۲۳ ریاضی دهم را با توضیح کامل مشاهده کنید و مشکلات خود را برطرف کنید. همچنین در ادامه مقاله نیز به این سوالات پاسخ داده شده است.

جواب کاردرکلاس صفحه ۱۲۲ و ۱۲۳ ریاضی دهم

الف) با سه رقم ۵ و ۳ و ۲ چند عدد سه رقمی می‌توان نوشت؟ به طور مثال ۲۳۵ و ۳۵۲ و ۳۳۵ سه نمونه از این اعدادند. برای این کار می‌توان نوشتن عدد سه رقمی را به صورت پرکردن سه جایگاه مقابل با ارقام مذکور در نظر گرفت.

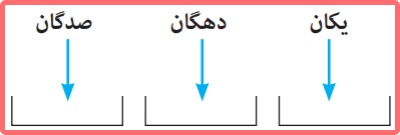
پس این کار سه مرحله دارد و هر سه مرحله آن باید انجام شود، برای به دست آوردن جواب، تعداد راه‌های پرکردن هر جایگاه باید مشخص شود و با استفاده از اصل ضرب در هم ضرب شود.

هر جایگاه را به سه حالت می‌توان پر کرد؛ لذا ۲۷ عدد وجود دارد.

با نمودار درختی در سال‌های ‌پیش آشنا شده‌اید. از این نمودار نیز می‌توان برای به دست آوردن تعداد اعداد مورد نظر و نیز نوعی از نمایش آنها استفاده کرد. به نمودار درختی کشیده شده در حاشیهٔ صفحه دقت و آن را تکمیل کنید.

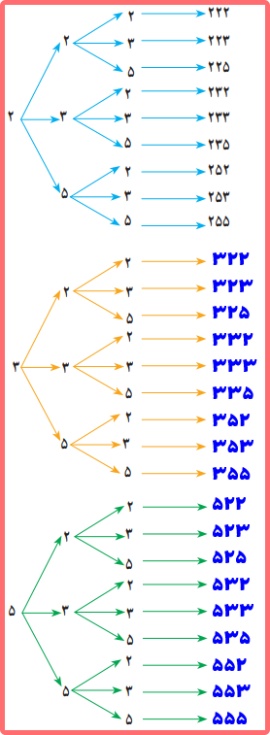
ب) با همان سه رقم چند عدد سه رقمی می‌توان ساخت که رقم تکراری نداشته باشد؟

پ) با همان سه عدد چند عدد سه رقمی زوج می‌توان نوشت؟

۱- جایگاه سمت راست به چند روش می‌تواند پر شود، به گونه‌ای که عدد ساخته شده زوج باشد؟
✅ جواب: به یک روش و فقط با عدد ۲ می تواند پر شود.

۲- دو جایگاه دیگر هر یک به چند روش می‌توانند، پر شوند؟
✅ جواب: دو جایگاه دیگر هر یک به 3 طریق می‌توانند پر شوند.
لذا تعداد اعداد در این حالت برابر است با ۹=۱×۳×۳

ت) با همان سه عدد چند عدد سه رقمی زوج با ارقام غیرتکراری می‌توان نوشت؟

۱- جایگاه سمت راست به چند روش می تواند پر شود به گونه ای که عدد ساخته شده زوج باشد؟
✅ جواب: به یک طریق و توسط عدد ۲ می تواند پر شود.

۲- پس از پرکردن جایگاه سمت راست، جایگاه سمت چپ، به چند طرق می تواند پر شود؟
✅ جواب: به ۲ طریق پر می شود.

۳- حال جایگاه وسط به چند طریق می تواند پر شود؟
✅ جواب: به یک طریق می تواند پر شود.

۴- لذا تعداد اعداد مورد نظر در این حالت برابر است با ۲=۱×۲×۱

⚠️ دانش آموز عزیز به این نکته نیز توجه داشته باشید که مطالب درسی قرار گرفته شده در این صفحه فقط جنبه کمک آموزشی دارد لذا قبل از استفاده کردن از آن ها حتما خودتان نیز به سوالات پاسخ دهید تا مفهوم درس را به خوبی متوجه شوید.

پاسخ صفحه قبلی: جواب صفحه ۱۲۱ ریاضی دهم

🔔 در این بخش جواب صفحه ۱۲۲ و ۱۲۳ ریاضی دهم که مربوط به فصل ۶ می باشد را مرور کردیم، اگر سوالی دارید از بخش نظرات بپرسید. جهت مشاهده پاسخ سایر تمرین های کتاب شماره صفحه آن را به همراه عبارت «ماگرتا» در گوگل جست و جو کنید.