جواب کاردرکلاس صفحه ۴۰ ریاضی نهم ✍️ با تدریس ویدیویی

جواب صفحه ۴۰ ریاضی نهم از فصل سوم، درس دوم «آشنایی با اثبات در هندسه» و پاسخ کاردرکلاس صفحه 40 ریاضی پایه نهم متوسطه را در ادامه در بخش آموزش و پرورش ماگرتا برای شما دانش آموز کوشا آماده کرده ایم.

پاسخ صفحه بعدی: جواب صفحه ۴۱ ریاضی نهم

توضیح صفحه 40 ریاضی نهم

در ویدیو زیر می توانید پاسخ کاردرکلاس صفحه 40 را با توضیح کامل مشاهده کنید و مشکلات خود را برطرف کنید. همچنین در ادامه مقاله نیز به این سوالات پاسخ داده شده است.

پاسخ کاردرکلاس صفحه ۴۰ و ۴۱ ریاضی نهم

به استدلال هایی دقت کنید که چهار دانش آموز برای مسئله زیر آورده اند:
مسئله: مجموع زاویه های داخلی مثلث ۱۸۰ درجه است.

استدلال حامد: حامد گفت یک مثلث متساوی الاضلاع را درنظر می گیریم؛ چون سه زاویه دارد و هر زاویه ۶۰ درجه است، مجموع زاویه های مثلث ۱۸۰ درجه است.

استدلال حسین: حسین چند مثلث مختلف با حالت های گوناگون کشید و زوایای آنها را اندازه گرفت و دید که در همه آنها مجموع زوایای داخلی برابر ۱۸۰ درجه است و نتیجه گرفت که مجموع زوایای داخلی هر مثلث ۱۸۰ درجه است.

استدلال مهدی: مهدی شکل روبرو را، که از مثلث های هم نهشت تشکیل شده است کشید و با مشخص کردن زاویه های مثلث ABC مانند شکل استدلالی با استفاده از شکل به صورت زیر آورد:

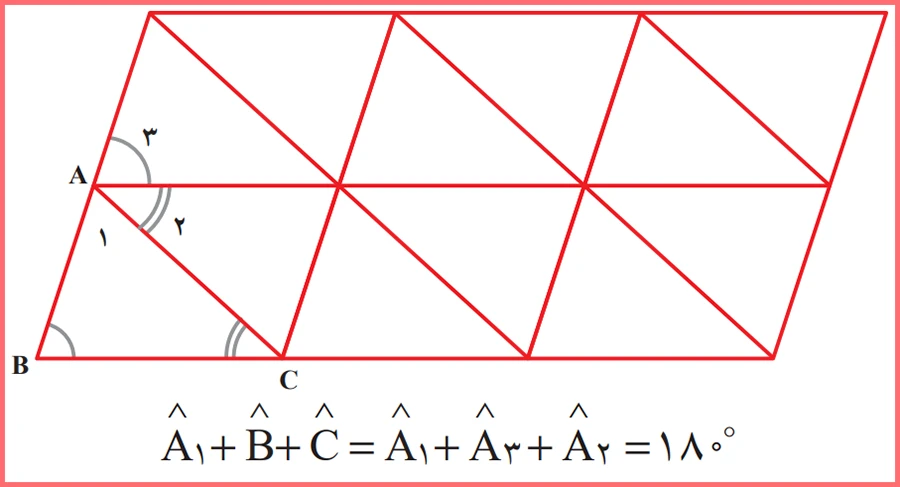
استدلال رضا: رضا گفت می دانیم که «هر خطی که دو خط موازی را قطع کند، با آنها هشت زاویه می سازد که مانند شکل چهار به چهار با هم مساوی‌اند».

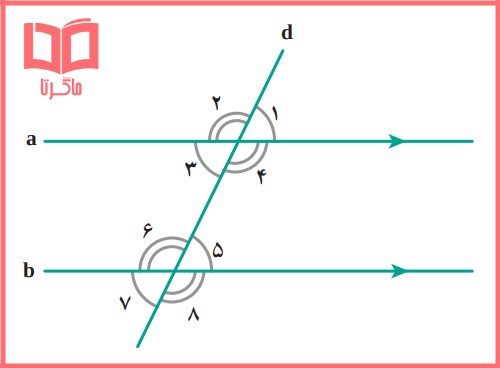
حال مثلثی دلخواه مانند ABC  را درنظر می گیریم؛ مانند شکل مقابل از راس A خط d را موازی BC رسم می کنیم.

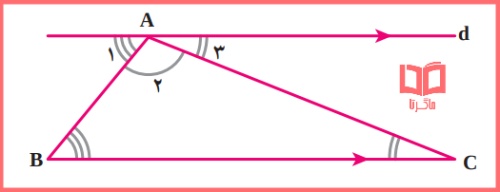
سه زاویه تشکیل شده در راس A را با شماره های ۱، ۲ و ۳ نشان داده ایم که زاویه A_۲  همان زاویه A در مثلث است و با درنظر گرفتن AB به عنوان مورب داریم: B = A_۱ و با درنظر گرفتن AC به عنوان مورب داریم : C = A_۳ پس با جای گذاری A_۱ و A_۳ به ترتیب به جای B و C خواهیم داشت : درجه A_۱+B+C = A۱+A۳+A۲ = ۱۸۰

استدلال رضا را می توان با استفاده از نمادهای ریاضی مرتب و خلاصه کرد و بدین صورت نوشت:

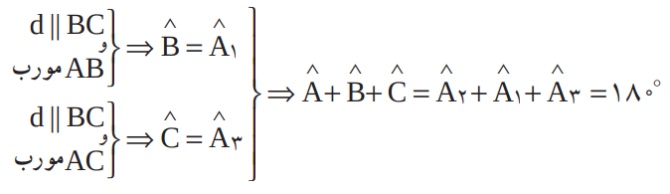
🔰 درباره معتبر بودن استدلال های این دانش آموزان بحث کنید.

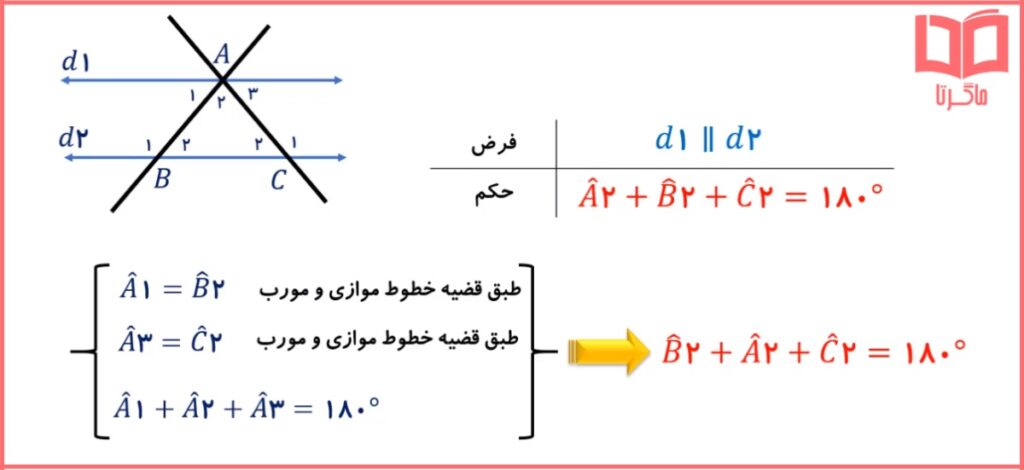
استدلال حامد: استدلال خوبی نیست زیرا فقط برای مثلث های متساوی الاضلاع (یک نوع مثلث خاص) درست است. آن هم در شرایطی که فرض ۶۰ درجه بودن هر زاویه در یک مثلث متساوی‌الاضلاع را قبول داشته باشیم.

استدلال حسین: این هم استدلال خوبی نیست زیرا حسین نمی تواند فقط با اندازه گیری چند مثلث نتیجه خود را به هر مثلثی تعمیم دهد. همچنین ممکن است مثلثی باشد که جمع زاویه های آن ۱۸۰ درجه نباشد. در واقع این راه خطای اندازه‌گیری دارد.

استدلال مهدی: در استدلال مهدی مشخص نیست که چطوری از کنار هم قرار گرفتن زاویه های مختلف مثلث های همنهشت، یک خط راست یا زاویه نیم صفحه تشکیل شده است. استدلال شهودی است و قابل استناد نیست.

استدلال رضا: رضا استدلال خوبی کرده است و با فرض های مسئله را حل کرده است که اثبات شده اند. همچنین استلال او به مثلث خاصی اختصاص ندارد و به هر مثلثی قابل تعمیم است. چهار زاویه تند باهم و چهار زاویه باز با هم مساویند.

در واقع، رضا با اتکا بر فرض‌های قطعی و روشی مشابه مهدی، مجموع زوایای داخلی مثلث را به مجموع سه زاویه در یک نیم‌صفحه تبدیل کرده است. با این حال، برتری استدلال رضا در مشخص بودن هم‌راستا بودن Ad با BC از همان ابتدا و همچنین ارائه یک اثبات منطقی و کلی برای همه مثلث‌هاست. این در حالی است که استدلال او بر پایه مفاهیم شناخته شده استوار بوده و به نوعی خاص از مثلث محدود نمی‌شود.

❤️ دانش آموز عزیز مطالب این صفحه صرفا جنبه کمک آموزشی دارد و شما برای استفاده از آن ها باید یک بار خودتان تمامی سوالات این صفحه را حل کنید سپس اگر مشکلی داشتید از این مطالب کمک بگیرید. با این کار در امتحان و پرسش های کلاسی دچار مشکل نخواهید شد.

پاسخ صفحه قبلی: جواب صفحه ۳۹ ریاضی نهم

🔚 اگر سوالی در رابطه با جواب کاردرکلاس صفحه ۴۰ ریاضی نهم دارید آن را از قسمت دیدگاه بپرسید. همچنین جهت مشاهده گام به گام سایر صفحات کتاب کافیست آن را به همراه عبارت «ماگرتا» در گوگل جست و جو نمایید.